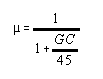
By Walter E. Lobo (Member) and James E. Evans! (Non-Member)
ABSTRACTA brief review of empirical equations for predicting heat transfer in the combustion chambers of steam boilers and petroleum heaters is followed by a study of eighty-five performance tests on nineteen furnaces differing widely in amount and arrangement of refractory cold surfaces. Operating conditions are available on furnaces with and without air preheat, with and without flue gas recirculation, fired with refinery cracked gas or oil fuel, and with a wide range of variation of excess air. The data are correlated by means of a theoretical equation and the deviations are no greater than the probable errors in the test data, and consistently less than those obtained by the empirical equation of Wilson, Lobo and Hottel. For simplicity of calculation the equation is presented in graphical form. An illustrative design problem has been included.
In view of the trend of the petroleum industry toward ever-increasing radiant heat transmission rates, as well as higher tube skin temperatures and higher percentages of heat-receiving surface per unit of refractory surface, this investigation has been initiated to study the effect of these variables and to find a means of allowing for their effect in the design of tubular oil heaters.
Eighty-five tests of nineteen different furnaces have been analyzed in this study. The test data include furnaces with and without air preheat and recirculation of flue gas. Excess air varied from 6% to over 170%, and average radiant rates from 3,000 to 54,000 Btu per hour per sq, ft. of circumferential tube area. The furnaces themselves were square, rectangular, or cylindrical in shape and varied widely in arrangement of surfaces; the ratio of effective refractory surface to equivalent cold plane surface varied from 0.45 to 6.55. Refinery cracked gas was the most common fuel, but a number of tests were made using oil fuel.
In this report a general and simple theoretical treatment is presented which satisfactorily correlates all the data. The deviations from the observed radiant section duties are well within the probable accuracy of the data. The average deviations of the predicted heat to the oil in the radiant section from the observed are 5.3% as compared to 6.85% when using the Wilson, Lobo, and Hottel empirical equation. The maximum deviation has been reduced from 33% to 16%. The data indicate that the larger deviations occurring when using the empirical equation are partly due to break-down of the equation below average radiant rates of 5,000 and above 30,000 Btu per hour per sq. ft. of circumferential area. It is likely that the empirical equation is seriously in error when applied to furnaces operating tube skin temperatures above 1000° F., as well as in furnaces having a low percentage of refractory surface and low values of PL, the product of partial pressure of the radiating constituents of the flue gas and the mean beam length of the radiating beam. The data available do not indicate any restriction which should be placed on the use of the theoretical equation herein presented.
*This paper is printed prior to presentation at the Thirty-Second Annual Meeting, Providence, Rhode Island, November 15, 16, and 17, 1939, in order to encourage discussion both verbal at the time of presenting and written.
Written discussion should be sent to the Secretary's Office promptly as it will be submitted to the author before publication. Written discussion received prior to November 10th will be read at time of presentation.
Discussion on this paper will be printed in Volume 36, No. 2, only.
!The M. W. Kellogg Company, New York City.
In view of the trend of the petroleum industry toward ever-increasing radiant heat transmission rates, as well as higher tube skin temperatures and higher percentages of heat-receiving surface per unit of refractory surface, this investigation has been initiated to study the effect of these variables and to find a means of allowing for them in the design of tubular oil heaters.
Although the exact mechanism of heat transmission in the radiant section of furnaces is complicated by factors about which little is known, certain generalizations and fundamental principles are fairly well established and can be used to advantage in solving radiant heat transfer problems. Some of these factors and their bearing on heat transfer problems are discussed below.
The major transfer of heat in the radiant section of a furnace is due to radiation from the hot gas cloud to the ultimate heat-receiving surface and by heat re-radiated from from the hot refractory surfaces to the cold surface. Some of the heat is also transferred at the instant of chemical union of the molecules in the flame. Of the radiation from the gas cloud, the major part is due to radiation from the carbon dioxide and water molecules present in it. Incandescent soot particles are a source of some radiation, but with fuels and burners commonly used in the petroleum industry, combustion usually results in a practically non-luminous flame. Oil fuels tend to give a more luminous flame than refinery gas at the usual percentages of excess air because of the cracking of the oil particles to soot during the combustion period. Data are not available on the exact degree of luminosity of oil flames, but it is probably a function of burner design, the amount of steam used in atomization and the percent excess air used.
In modern furnaces increasing amounts of heat are transmitted directly from the gas mass and lesser amounts are transmitted by the way of the refractory because the current trend is to fill the radiant section with cold tube surface in the interest of economy. Since the radiating constituents in the flue gas are the H2O, CO2 and SO2 molecules present, the amount of heat radiated by them will be a function of their number and the temperature of the gas and cold surfaces. One measure of their number is their partial pressure. Another measure of their number is the mean length of the radiating beam in the gas mass. Hottel 1 has shown that the product PL, atmospheres-feet, expresses these two facts and permits the data on the radiation from gases to be correlated. For any given fuel, P is a function of the excess air used and L is a function of the furnace alone. An equation, to be valid for a wide variety of sizes and shapes of furnaces, must take into account the effect of PL on furnace performance.
Heat transfer by convection to the tubes in the radiant section of petroleum heaters accounts for only a small amount of the heat transferred, especially in high radiant rate furnaces. This convection transfer is more important in low rate furnacesbecause heat transfer by convection is proportional to the temperature difference Tg - Ts, between flue gas and cold surface, whereas the radiant heat transfer is proportional to the difference T4g - T4s where the temperatures are expressed as degrees Rankine.
In view of the complexity of the problem, numerous investigators have correlated furnace performance by means of empirical equations. To illustrate the basic approach several of these empirical treatments are briefly summarized and their outstanding limitations described. A more complete review of this earlier lititure has been made in a previous publication.2
The following empirical equations have been classified into two major groups according to whether they are similar to the Hudson or the DeBaufre type equation.
Hudson3 correlated the data on several types of steam-boiler furnaces by the simple equation:
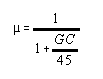
|
(1) |
m = fraction of total heat input to the furnace (above the steam temperature) which
is absorbed by the ultimate heat receiver.
G = air-fuel ratio, lbs. air / lb. fuel fired
C = pounds of fuel per hour per sq. ft. of water-cooled surface.
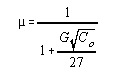
|
(2) |
m = fraction of heat transferred above atmospheric temperature
G = air-fuel ratio, lbs. air / lb. fuel fired
Co = pounds of equivalent good bituminous coal per hour per sq. ft. of water-cooled surface.
Wilson, Lobo and Hottel 2 modified the Orrok equation and correlated the performance on ten of twelve furnaces. Their recommended equation is :
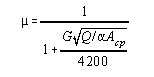
|
(3) |
m = fraction of total heat input above 60°F. absorbed by the cold surface
a Acp = effectiveness of tube surface as compared to a continuous
cold plane, sq. ft.
Q = net heat liberated from combustion of the fuel, B.t.u. per hour
G = air-fuel ratio, lbs. air per lb. fuel fired.
Hottel 5 has proposed the following type of equation :
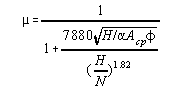
|
(4) |
H = total net heat input from all sources, B.t.u. per hour
N = the hourly mean heat capacity of the flue gas between the temperature of the gas leaving the chamber
and a base temperature of 60° F. B.t.u./hour/°F.
f = an overall exchange factor defined by the equation :
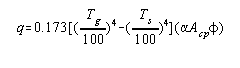
|
(5) |
where
q = heat transferred by radiation, B.t.u./hour
Tg = temperature of the gas or hot surface, °F. + 460
Ts = temperature of cold surface, °F. + 460.
The overall exchange factor makes allowance for variation in effective flame emissivity, arrangement of refractory and non-black conditions in the furnace chamber. The constants in the above equation are very tentative so that it is only to be considered as illustrating a method. The f concept has been satisfactorily used in the equation presented in this paper and has been defined and discussed under the derivation of the theoretical equation.
DeBaufre 6 proposed an empirical equation which is similar to the basic Stefan-Boltzmann equation :
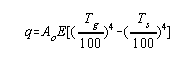
|
(6) |
q = heat transferred, B.t.u./hour
Ao = total tube surface exposed to radiation, sq. ft.
Tg = temperature of the products of combustion leaving the furnace chamber, °F. + 460
Ts = temperature of cold surface, °F. + 460
E = effectiveness factor of the cold surface.
DeBaufre attempted to correlate E as a function of the rate of heat liberation per unit of furnace volume but the correlation was poor. For black body conditions E would have a maximum value of 0.173, the Stefan-Boltzmann constant.
Mekler 7 proposes the equation :
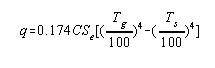
|
(7) |
q = heat transferred by radiation, B.t.u./hour
Se = equivalent "effective" heating surface, sq. ft.
C = an empirical coefficient depending on the temperature used for Tg
Tg = exit gas or theoretical flame temperature, °F. + 460
Ts = temperature of cold surface, °F. + 460.
In contrast to DeBaufre, however, he evaluates Se as a function of the "fraction cold" of the furnace. An approximate graphical method is used for solving the DeBaufre type of equation. No cognizance is taken of the effect of PL on the heat transferred, and furnaces having the same geometric shape but widely different volumes are presumed to have the same fractional heat absorbtion. The effect of excess air on flame emissivity is likewise neglected.
If a series of furnaces operate on fuels whose heating value varies between comparatively narrow limits and whose ultimate heat-receiving surface temperatures are nearly constant, the performance of these furnaces may be adequately described by a simple empirical equation. However, as conditions deviate from those used to determine the constants of the equation its validity will be questionable. For example, a valid equation determined for tubes at a low temperature will certainly be invalid when the tube temperature is increased to a much higher value because as this temperature is increased it becomes more difficult to transfer a given amount of heat in a given furnace. In other words, to maintain a definite radiant rate in a furnace with a high tube temperature, more fuel must be fired.
Another disadvantage of the empirical equation is the difficulty of allowing for the effect of excess air unless a fuel of approximately constant heating value is used. If, for example, an air-fuel ratio is used to measure the effect of air addition, large values of the ratio are commonly associated with high percentages of excess air and low available heats. Conversely, small values of the ratio are associated with low percentages of excess air and high available heats. The danger involved in the indiscriminate use of an air-fuel ratio is best illustrated by an example. For theoretical combustion an average blast furnace gas would have an air-fuel ratio of approximately 0.73 lbs. air per lb. fuel gas and a natural gas might have a ratio of 15.9, yet the theoretical flame temperature of the blast furnace gas would be only 2800° F. as compared to 3580° F. for the natural gas. If the excess air in the case of the combustion of the blast furnace gas were increased until the air-fuel ratio became 15.9, the theoretical flame temperature would drop to a temperature much lower than 2800° F. If the the tube temperature was then increased, a point would be reached where no heat could be transferred to the tubes. However, with the same net heat liberation, natural gas fuel would transfer a finite amount of heat.
Realizing the limitations of the purely empirical approach it was decided to develop a theoretical radiant heat equation, simplified by assumptions, if necessary, and to test it by the application to* data obtained on furnace performance.
*It should be remembered, however, that in many furnaces the usual measurement of the temperature of the gases leaving the radiant section does not give Tg directly, but a value usually less than Tg depending on the quantity of heat lost by the flue gases to the convection section by radiation at the point of measurement.
By a proper definition of terms the heat transferred in the radiant section could be predicted exactly by a Stefan-Boltzmann type equation.
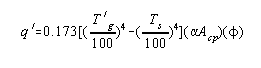
|
(8) |
q' = net heat transferred by radiation to the tubes, B.t.u./hour
T'g = mean temperature of the hot gases in the furnace, °F. + 460
T's = mean tube skin temperature, °F. + 460.
a Acp = area of a plane which will absorb the same as the actual
cold surface in the furnace, sq. ft.
f = an overall exchange factor correcting for flame emissivity, arrangement of the
refractory, volume of the combustion chamber, etc. This factor will be discussed in detail later.
In the combustion chamber Tg, the mean temperature of the hot gases in the furnace and the temperature of the exit gases will undoubtedly differ, but run somewhat parallel. However, it was assumed that T'g
could be replaced by the exit temperature, Tg.* This assumed interchangeability introduces, of course, a degree of empiricism into the equation which will be justified, however, if the results are satisfactory.All the net heat transferred to all the surfaces in the radiant section, i.e., the heat lost by the flame, is given by the following equation :
 |
(9) |
A'r = area of refractory in furnace, sq. ft.
Ao = circumferential tube surface, sq. ft.
hc = convection coefficient, B.t.u./hour/sq.ft./°F.
Since both the external losses from the furnace and the net heat transferred to the refractory by convection, given by the term hcA'r(Tg - Tr), are usually small, the two may be assumed equal without appreciably affecting the results. Equation (9) may then be rewritten to give instead the heat received by the oil :
 |
(10) |
The second term represents the heat transferred to the tubes by convection and it may be approximated as its magnitude is usually much smaller than the first term of equation (10).
By making the assumptions that :
| 1. The convection coefficient lies normally between 2 and 3 B.t.u./hour/sq.ft./°F.; | |
| 2. In most furnaces Ao equals (2a Acp) approximately; | |
| 3. The overall exchange factor f has a value of about 0.57; |
 |
(11) |
Making this substitution in equation (10) :
 |
(12) |
Of the various ways that equation (12) representing the heat transfer relation can be combined with the equation representing a heat balance on the combustion chamber, the following graphical procedure is suggested :
Let
| H = the total net heat input to the furnace from all sources; i.e., combustion of the fuel, sensible heat in the air and fuel, sensible heat in recirculated flue gases, etc., B.t.u./hr. | |
| q = the total net heat absorbed in the radiant section by the ultimate heat-receiving surface, B.t.u./hr. | |
| N = the hourly heat capacity of the flue gas evaluated at the temperature of the gasses leaving the section, B.t.u./hr./°F. = (mols/hours) (mean MCp between tg and 60°F.) (see Figure No. 15 in Appendix) | |
| b = fraction of total net heat input lost from the external furnace walls | |
| tg = temperature of the gases leaving the section, °F. | |
| bH = total heat losses, B.t.u./hr. |
The heat balance equation may be written : (Datum temperature = 60° F.)
| (13) |
By multiplying both sides of the equation by H(1 - b) we obtain :
| (14) |
Then
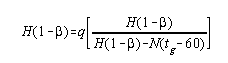
|
(15) |
This may be transposed to :
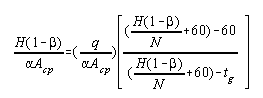
|
(16) |
The merit of such a relation is that the term in parentheses in the brackets is dependent on the fuel characteristics, excess air, air preheat, etc., and may be separately evaluated. After its value is determined, it may be used to establish the simple graphical relation among H((1 - b))/ aAcp, q/aAcp, tg, in accordance with the following construction :
 |
Since the term (t'f - 60) is, from its method of construction the theoretical temperature the gases would attain (a) if combustion were adiabatic except for the loss of the fraction b of the enthalpy of the fuel and (b) if the products of combustion had a mean specific heat equal to their mean value from tg down to the base temperature, the term t'f may be thought of as a sort of flame temperature, referred to hereafter as the pseudo-flame temperature for short.
If now a plot is constructed with the coordinates q/aAcp and tg' a series of lines representing equation (12) may be placed on the plot; one for each value of surface temperature ts (see Figures 1 and 2). On the same diagram a straight line through the value t'f (completely determined by fuel characteristics, and presented for varying conditions of operation in Figures 3 and 4 in which the radiant section external losses have been taken as 2% of the total net heat input to the furnace) drawn through a point on the family of curves corresponding to the correct tube skin temperature, ts, and for q/aAcp or tg (according to which of these is fixed) when extended to the left, will intersect the line tg=60° at the value of H((1 - b))/aAcp.
 |
 |
 |
 |
In design calculations the temperature, tg, of the flue gases leaving the radiant section must be estimated before the pseudo-flame temperature can be obtained. This assumed or provisional t'f must be revised if the assumed bridge wall temperature is found to be considerablely in error. The descriptive example included at the end of this section illustrates the method of calculation.
Acp is the area of a continuous plane replacing the row of tubes and may be taken as the product of the exposed tube length, and center to center distance between tubes, and the number of tubes in the exposed radiant row. a is the ratio of reception by the actual surface to reception by a continuous plane. Then the term aAcp is the tube area expressed as equivalent cold plane surface, i.e., the area of a plane which will absorb the same as the actual cold surface in the furnace.
Hottel8 gives a as a function of the ratio
as in Figure 5.
| The following example illustrates the method of calculating a Acp. | ||
| Assume a radiant section of the following characteristics : | ||
| Size of tubes | 5" outside diameter | |
| Center to center distance of tubes | 10" | |
| Exposed length of tube | 30 ft. | |
| Total number of tubes | 60 | |
| Arrangement of tubes, 2 rows on equilateral triangular spacing | ||
| Number of tubes per row | 30 | |
| a=0.984, i.e., total to 2 rows | ||
| aAcp=0.984(750)=738 sq.ft. equivalent cold plane surface. | ||
 |
| Fig. 5 Distribution of Heat to One or Two Rows of Tubes Mounted on |
| Refractory Wall and Irradiated from One Side. |
Tubes on equalateral triangular centers; ordinate expressed on basis of heat transfered from a plane to a plane replacing tubes, or to infinite number of rows of tubes. These curves are a good approximation for tubes placed on rectangular or square centers
By definition, the emissivity of the flame is the ratio of the heat actually transmitted from the flame to the cold surface to the heat which would have been transmitted had the flame and the cold surface been perfect radiators. An illustrative example of this calculation is available in the literature.11
 |
Figure No. 6 gives Pf in terms of (PCO2+PH2O)L, tg, and ts for cracked gas fuel and a tube emissivity of 0.90. This plot is also a good approximation for fuel oil. The radiation cjharts of Hottel9 which were used in this calculation are included in the Appendix as Figures Nos. 13 and 14.
| PCO2 | = | partial pressure of carbon dioxide in the flue gas, atmospheres |
| PH2O | = | partial pressure of water vapor in the flue gas, atmospheres |
| L | = | mean length of radiant beam in the combustion chamber, feet |
| PL | = | atmospheres-feet |
 |
Values of PCO2 + PH2O and the air-fuel ratio for typical cracked gas and oil fuels have been plotted on Figure No. 7. The analysis of the fuels on which these calculations are based are indicated in the Appendix.
The mean length, L, of the radiant beam in the combustion chamber may be estimated from Table I.
| Table I.-Mean Length of Radiant Beams in | ||||
| Various Gas Shapes12 | ||||
| From the values given by Hottel12 for the mean length, L, of radiant beams | ||||
| in various gas shapes, the following approximate values have been | ||||
| derived for use in practical oil heater design. These values | ||||
| may be used until more exact methods are available. | ||||
| Dimensional Ratio | ||||
| (length, width, height | L | |||
| in any order) | ||||
| Rectangular Furnaces | ||||
| 1. | 1-1-1 | to | 1-1-3 | |
| 1-2-1 | to | 1-2-4 | 2/3(Furnace Volume)1/3 | |
| 2. | 1-1-4 | to | 1-1-inf | 1 x smallest dimension |
| 3. | 1-2-5 | to | 1-2-8 | 1.3 x smallest dimension |
| 4. | 1-3-3 | to | 1-inf-inf | 1.8 x smallest dimension |
| Cylindrical Furnaces | ||||
| 5. | d x d | 2/3 x diameter | ||
| 6. | d x 2d | to | d x inf | 1 x diameter |
| Let | ||
| At | = | total area of furnace surfaces in the radiant section= |
| Acp + refractory surfaces unprotected by tubes, sq. ft | ||
| aAcp | = | equivalent cold plane surface, sq.ft. |
| Ar | = | effective refractory surface, sq.ft. (Ar = At - aAcp) |
| Pc | = | emissivity of the ultimate heat-receiving surface, assumed |
| =0.90 | ||
| Pf | = | emissivity of the flame. |
| Frc | = | fraction of all the radiation emitted from all the refractory |
| in all directions, which, if not absorbed by the gas, | ||
| would hit cold surface aAcp |
The overall exchange factor, f, as defined by Hottel9, is then :
 |
(18) |
Where
 |
(19) |
Af = Area of the flame bundle, sq. ft.
In commercial furnaces Af may be considered equal to At, and equation (19)
may be simplified to the form used in this study :
 |
(20) |
The exact evaluation10 of Frc is rather tedious. In an effort to simplify the evaluation of this factor, more than twenty furnaces differing as widely as possible in design were studied, using the exact technique referred to above. It was found that for ratios of Ar/aAcp from 0 to 1, the value of Frc was adequately given by the ratio aAcp/At. For ratios of Ar/aAcp from 3 to 6.5, Frc was very nearly equal to aAcp/Ar. Figure No. 8 embodies these results and gives f directly as a function of the ratio Ar/aAcp and the flame emissivity Pf.
Before discussing the results which prove the validity of the assumptions made in the development of the radiant equation, a descriptive example will be given to illustrate the use of the general method.
Find the total net heat input (i.e., the enthalpy of the incoming fuel and air above 60° F., water as vapor) to the following furnace :
| Data | |
| Dimensions of combustion chamber | 15' x 30' x 40' |
| Tube outside diameter | 5: O.D. |
| Center to center spacing | 10" |
| Number of tubes in section | 90 arranged in a single row |
| Circumferential tube surface | 4710 sq. ft. |
| Total wall area, Ar | 4300 sq. ft. * |
| Conditions | |
| Net heat input to oil | 70,650,000 B.t.u./hr. |
| Desired radiant rate | 15,000 B.t.u./hr./sq.ft. circumferential surface |
| Cracked gas fuel | 20,000 B.t.u./lb. (L.H.V.) |
| Excess air | 30% |
| Temperature of air leaving preheater | 460° F. |
| Estimated tube skin temperature | 1000° F. |
| Calculation of effective surface, aAcp | Reference | |
| Center to center distance/tube O.D. | 2 | |
| a to one row | 0.88 | Fig. 5 |
| Acp = (90 tubes)(10"C/12)(40' long) | 3,000 sq.ft. of Acp | |
| aAcp = 0.88(3000) | 2,640 sq.ft. of aAcp | |
| Calculation of exchange factor, f | ||
| Radiant section dimension ratio, 15/15 x 30/15 x 40/15 = 1 x 2 x 2.67 | ||
| L = 2/3(volume)1/3 = 2/3(15x30x40)1/3 | 17.5 feet | Table I |
| P, partial pressure CO2 + H2O | 0.22 atmospheres | Fig. 7 |
| PL = 0.22(17.5) | 3.84 (atm.) (ft.) | |
| Assume tg (temp. flue gas leaving) | 1,800° F. | |
| PF, flame emissivity | 0.495 | Fig. 6 |
| AR = Ar-aAcp = 4300-2640 | 1,660 sq.ft. | |
| AR/aAcp = 1600/2640 | 0.63 | |
| f = | 0.56 | Fig. 8 |
| q/aAcp f = 15,000(4710/2640)(1/0.56) | 47,900 B.t.u./hr./aAcp f | |
| Calculation of Total Net Heat Input | Results | Reference |
| tg | 1,850° F. | Fig. 2 |
| PF, as previously calculated ** is close enough | 0.495 | |
| t'F at 30% excess air, 460-60=400° | ||
| air preheat, 1850° F. tg | 3,620° F. | Fig. 3 |
| 0.98 H/aAcp f | 94,000 B.t.u./hr./aAcp f | Fig. 2 |
| H/aAcp (94,000/0.98) x 0.56 | 53,700 B.t.u./hr./aAcp | |
| H = Total net heat input (53,700)(2,640) | 142,000,000 B.t.u./hr. | |
| * Area of opening to convection section equals 200 sq.ft. so Ar = 4500-200. | ||
| ** When assumed temperature of flue gases leaving radiant section is in | ||
| error by 100° or more, PF and f should be revised. | ||
The results of the investigation are summarized in Tables II and III. Table II gives the characteristics of the furnaces studied and the ratio of the actual heat to the oil to that calculated by the proposed theoretical equation, as well as by the empirical equation of Wilson, Lobo and Hottel. Sketches of the general types of furnaces studied are shown in Figures 16 through 22 in the Appendix. These should be considered as diagrammatic only.
| Table II. - Characteristics of Furnaces and Tests | |||||||||||||||
| Total | Total | Mean | Ratio: | ||||||||||||
| Tube | Circum | Effective | Furnace | Effective | Length | ||||||||||
| Outside | Tube | ferential | Tube | Wall | Refractory | Ratio | Radiant | Air | Flue Gas | No.of | Actual/Calculated | ||||
| Furnace | Diameter | Spacing | TubeArea | Area | Surface | Surface | AR/Acp | Beam | Preheat | Recirculation | Fuel | Tests | Heat to Oil | ||
| (h) | (g) | ||||||||||||||
| Symbol | General | O.D. | C-C | Ac | aAcp | AT | AR | L | Empirical | Theoretical | |||||
| Unit | Type | Inches | Inches | Sq.Ft. | Sq.Ft. | Sq.Ft. | Sq.Ft. | Feet | Equation | Equation | |||||
| *1 | A | 5 | 10 | 2,389 | 1,340 | 3,080 | 1,740 | 1.30 | 14.3 | Yes & No | Yes & No | Gas | 16 | 1.03 | 1.02 |
| *2 | B | 4 | 6.75 | 1,496 | 756 | 3,271 | 1,515 | 2.00 | 19.6 | Yes | No | Oil | 17 | 0.93 | 0.94 |
| *3 | C | 5 | 10 | 2,945 | 2,255 | 3,855 | 1,600 | 0.71 | 17.0 | No | Gas | 10 | 0.95 | 0.99 | |
| 4 | B | 5 | 10 | 2,394 | 1,343 | 4,277 | 2,934 | 2.18 | 17.8 | Yes | No | Gas | 7 | 0.94 | 0.97 |
| *5 | D | 5 | 17.3(a) | 4,443 | 2,303 | 3,362 | 1,059 | 0.46 | 24.0(c) | Yes | No | Gas | 3 | 0.92 | 1.00 |
| 6(d) | E | 5 | 9 | 3,060 | 1,608 | 3,174 | 1,566 | 0.97 | 12.8 | No | No | Gas | 2 | 1.02 | 0.99 |
| 7(d)#1 | E | 5.5 | 9.75 | 12,467(b) | 3,610 | 6,560 | 2,950 | 0.82 | 22.2 | No | No | Gas | 1 | 1.18 | 1.11 |
| 7 #2 | E | 5 | 9.25 | 7,153 | 3,698 | 6,560 | 2,862 | 0.77 | 22.2 | No | No | Gas | 1 | 1.11 | 1.14 |
| *8 | F | 4 | 8.75 | 284 | 216 | 1,628 | 1,412 | 6.55 | 11.2 | No | No | Gas | 7 | 1.04 | 0.98 |
| 9 | B | 5 | 8.75 | 4,775 | 1,844 | 2,976 | 1,132 | 0.61 | 14.7 | Yes | No | Gas | 4 | 1.04 | 1.03 |
| 10 | G | 4 | 8.75 | 1,347 | 465 | 1,875 | 1,410 | 3.04 | 11.2 | No | No | Oil | 3 | 0.94 | 0.99 |
| 11 | G | 4 | 8.75 | 1,466 | 498 | 1,608 | 1,110 | 2.23 | 8.28(e) | No | No | (f) | 3 | 0.77 | 1.07 |
| 12 | B | 5 | 8.75 | 2,314 | 1,197 | 3,423 | 2,226 | 1.86 | 15.9 | No | No | Oil | 2 | 0.98 | 1.08 |
| 13 | D | 5 | 10.25 | 5,780 | 2,108 | 3,333 | 1,225 | 0.58 | 22.5(c) | Yes | No | Gas | 1 | 1.02 | 0.99 |
| 14 | D | 5 | 10.25 | 5,780 | 2,108 | 3,049 | 941 | 0.45 | 22.5(c) | Yes | No | Gas | 1 | 0.94 | 0.91 |
| 15 | D | 5 | 10.25 | 2,890 | 1,928 | 3,067 | 1,139 | 0.59 | 22.5(c) | Yes | No | Gas | 1 | 0.99 | 0.93 |
| 16 | D | 5 | 10.25 | 5,780 | 2,108 | 3,049 | 941 | 0.45 | 22.5(c) | Yes | No | Gas | 1 | 0.99 | 0.98 |
| 17 | B | 5 | 8.75 | 1,718 | 887 | 2,369 | 1,482 | 1.67 | 13.2 | No | No | Gas | 1 | 0.92 | 0.94 |
| 18 | B | 5 | 8.75 | 1,867 | 965 | 2,143 | 1,178 | 1.22 | 12.6 | No | No | Gas | 3 | 0.96 | 1.02 |
| 19 | E | 5.5 | 9.25 | 3,616 | 1,820 | 3,885 | 2,065 | 1.14 | 17.1 | No | No | Oil | 1 | 0.90 | 1.08 |
| FOOTNOTES : | |||||||||||||||
| (a) | Two rows with center lines 2.62 inches apart. | ||||||||||||||
| (b) | Double row of tubes. | ||||||||||||||
| (c) | Circular furnace, L = diameter. | ||||||||||||||
| (d) | Double radiant type furnace. | ||||||||||||||
| (e) | L = 1.8 (minimum distance). | ||||||||||||||
| (f) | Products of combustion from furnace No. 10. | ||||||||||||||
| (g) | Wilson, Lobo, and Hottel Empirical Equation. | ||||||||||||||
| (h) | For sketches of general type of furnace see Figs. 16 through 22 in the Appendix. | ||||||||||||||
| * | Furnaces used by Wilson, Lobo and Hottel (2). | ||||||||||||||
| Table III. - Test Data and Calculations | |||||||||||||||||||
| (b) | RadiantSection | (c) | Rate of Heat | Ratio:Actual/Calculated | |||||||||||||||
| Average | (a) | Bridge | Temperatures | Average | (d) | (e) | Input | Absorption | Heat to Oil | ||||||||||
| Radiant | Excess | Wall | Tube | Overall | TotalNet | Hourly | Pseudo- | Heat | (g) | ||||||||||
| Symbol | Furnace | RateTo | Air | Temper- | Oil | Oil | Skin | Flame | Exchange | Heat | Heat | Flame | into | 0.98H | q | Empirical | Theoretical | ||
| Unit | Fuel | Test | FirstRow | ture | In | Out | Temp. | Emissivity | Factor | Input | Capacity | Temp. | Oil | aAcp f | aAcp f | Equation | Equation | ||
| B.t.u./hr./ | t'g | ts | H | N | t'f | q | |||||||||||||
| Sq.Ft. | % | °F. | °F. | °F. | °F. | Pf | f | 106B.t.u./hr. | Btu/hr/°F | °F. | 106B.t.u./hr. | 106B.t.u./hr. | |||||||
| 1 | Gas | 1 | 4,760 | 17.3 | 1,140 | 728 | 850 | 820 | 0.525 | 0.675 | 53.04 | 34,643 | 1,562 | 11.4(f) | 57.40 | 12.60 | 1.04 | 1.01 | |
| 2 | 6,440 | 113.8 | 1,220 | 700 | 865 | 817 | 0.415 | 0.585 | 42.21 | 21,528 | 1,980 | 15.4 | 52.80 | 19.60 | 1.04 | 1.14 | |||
| 3 | 7,190 | 80.8 | 1,250 | 680 | 868 | 805 | 0.456 | 0.621 | 37.68 | 16,692 | 2,275 | 17.2 | 44.50 | 20.60 | 1.24 | 1.12 | |||
| 4 | 7,650 | 72.3 | 1,250 | 675 | 875 | 809 | 0.460 | 0.625 | 37.55 | 15,246 | 2,475 | 18.3 | 43.80 | 21.80 | 1.12 | 1.11 | |||
| 5 | 9,110 | 51.0 | 1,230 | 645 | 875 | 788 | 0.480 | 0.645 | 35.25 | 10,196 | 3,455 | 21.8 | 40.40 | 25.35 | 1.07 | 1.06 | |||
| 7 | 8,900 | 48.9 | 1,180 | 648 | 872 | 794 | 0.494 | 0.650 | 36.18 | 9,672 | 3,720 | 20.8 | 40.60 | 23.35 | 0.99 | 0.94 | |||
| 8 | 7,990 | 32.4 | 1,180 | 660 | 870 | 794 | 0.514 | 0.665 | 36.57 | 11,942 | 3,060 | 19.1 | 40.35 | 21.43 | 1.01 | 0.97 | |||
| 9 | 7,480 | 61.1 | 1,200 | 660 | 858 | 790 | 0.480 | 0.640 | 35.86 | 11,548 | 3,100 | 17.9 | 40.70 | 20.85 | 1.05 | 0.93 | |||
| 10 | 6,440 | 122.0 | 1,215 | 680 | 850 | 795 | 0.419 | 0.590 | 38.05 | 17,211 | 2,225 | 15.4 | 47.10 | 19.43 | 0.98 | 1.04 | |||
| 11 | 6,260 | 141.3 | 1,225 | 685 | 850 | 797 | 0.412 | 0.585 | 39.22 | 16,438 | 2,395 | 15.0 | 49.10 | 19.10 | 1.04 | 0.92 | |||
| 12 | 5,440 | 178.0 | 1,225 | 700 | 843 | 803 | 0.395 | 0.565 | 44.32 | 22,715 | 1,970 | 13.0 | 57.00 | 17.07 | 0.94 | 0.93 | |||
| 15 | 9,560 | 33.3 | 1,360 | 650 | 858 | 780 | 0.498 | 0.655 | 44.46 | 14,954 | 2,960 | 22.9 | 49.60 | 26.50 | 1.04 | 1.06 | |||
| 16 | 11,030 | 30.5 | 1,440 | 650 | 885 | 793 | 0.485 | 0.641 | 51.22 | 16,889 | 3,040 | 26.4 | 58.40 | 30.75 | 0.99 | 1.05 | |||
| 17 | 10,700 | 26.0 | 1,360 | 655 | 885 | 800 | 0.505 | 0.660 | 47.49 | 16,499 | 2,880 | 25.6 | 52.70 | 29.00 | 1.01 | 1.12 | |||
| 18 | 6,470 | 24.4 | 1,250 | 728 | 865 | 822 | 0.520 | 0.670 | 65.32 | 36,228 | 1,823 | 15.5 | 71.15 | 17.24 | 0.91 | 0.95 | |||
| 19 | 10,200 | 42.1 | 1,270 | 655 | 875 | 795 | 0.485 | 0.642 | 45.72 | 12,843 | 3,550 | 24.4 | 52.00 | 28.35 | 0.95 | 0.96 | |||
| Avg | .... | 1.03 | 1.02 | ||||||||||||||||
| 2 | Oil | 1 | 7,160 | 114 | 1,270 | 681(b) | 717 | 0.49 | 0.720 | 24.58 | 10,300 | 2,395 | 10.73 | 44.10 | 19.72 | 0.99 | 1.00 | ||
| 2 | 4,200 | 184 | 1,260 | 688 | 715 | 0.501 | 0.780 | 20.94 | 11,300 | 1,873 | 6.30 | 37.10 | 11.70 | 0.77 | 0.87 | ||||
| 3 | 4,840 | 154 | 1,225 | 689 | 717 | 0.494 | 0.725 | 19.55 | 9,560 | 2,065 | 7.24 | 34.90 | 13.18 | 0.87 | 0.91 | ||||
| 4 | 7,720 | 38 | 1,415 | 692 | 726 | 0.585 | 0.772 | 23.55 | 7,640 | 3,080 | 11.58 | 39.40 | 19.78 | 0.91 | 0.90 | ||||
| 5 | 7,520 | 30 | 1,410 | 694 | 725 | 0.643 | 0.800 | 22.16 | 7,060 | 3,130 | 11.24 | 35.80 | 18.59 | 0.92 | 0.91 | ||||
| 6 | 7,890 | 51 | 1,450 | 702 | 735 | 0.570 | 0.770 | 25.46 | 8,690 | 2,935 | 11.80 | 42.90 | 20.20 | 0.91 | 0.89 | ||||
| 7 | 7,600 | 74 | 1,420 | 703 | 733 | 0.556 | 0.763 | 26.71 | 10,180 | 2,535 | 11.39 | 45.20 | 19.70 | 0.89 | 0.94 | ||||
| 8 | 7,590 | 83 | 1,440 | 704 | 735 | 0.541 | 0.750 | 27.78 | 10,540 | 2,640 | 11.36 | 47.70 | 20.00 | 0.89 | 0.89 | ||||
| 9 | 4,800 | 175 | 1,175 | 699 | 730 | 0.512 | 0.735 | 19.28 | 10,000 | 1,950 | 7.18 | 33.80 | 12.89 | 0.94 | 0.98 | ||||
| 10 | 5,100 | 167 | 1,205 | 702 | 736 | 0.502 | 0.730 | 20.23 | 10,200 | 2,002 | 7.64 | 35.95 | 13.82 | 0.94 | 0.97 | ||||
| 11 | 4,920 | 69 | 1,200 | 680 | 716 | 0.585 | 0.772 | 14.58 | 5,650 | 2,590 | 7.37 | 24.40 | 12.61 | 0.94 | 0.95 | ||||
| 12 | 5,180 | 48 | 1,205 | 677 | 717 | 0.610 | 0.785 | 14.30 | 5,080 | 2,820 | 7.75 | 23.60 | 13.02 | 0.95 | 0.96 | ||||
| 13 | 5,050 | 100 | 1,185 | 692 | 728 | 0.557 | 0.763 | 16.13 | 6,860 | 2,363 | 7.55 | 27.40 | 13.08 | 0.95 | 0.96 | ||||
| 14 | 5,320 | 120 | 1,225 | 698 | 735 | 0.517 | 0.740 | 17.84 | 7,820 | 2,300 | 7.96 | 31.20 | 14.20 | 0.96 | 0.97 | ||||
| 15 | 6,500 | 106 | 1,270 | 694 | 726 | 0.525 | 0.743 | 23.40 | 10,120 | 2,323 | 9.73 | 40.70 | 17.30 | 0.94 | 0.96 | ||||
| 16 | 6,780 | 42 | 1,230 | 679 | 716 | 0.584 | 0.770 | 18.54 | 6,340 | 2,920 | 10.14 | 31.15 | 17.40 | 0.99 | 0.99 | ||||
| 17 | 6,740 | 68 | 1,300 | 684 | 720 | 0.561 | 0.768 | 20.64 | 7,630 | 2,720 | 10.09 | 35.15 | 17.48 | 0.97 | 0.96 | ||||
| Avg | .... | 0.93 | 0.94 | ||||||||||||||||
| 3 | Gas | 1 | 8,360 | 55 | 1,390 | 749 | 927 | 884 | 0.475 | 0.557 | 46.93 | 15,300 | 3,060 | 24.66 | 36.60 | 19.60 | 0.98 | 0.99 | |
| 2 | 8,000 | 105 | 1,430 | 765 | 923 | 889 | 0.425 | 0.517 | 56.41 | 22,700 | 2,493 | 23.61 | 47.40 | 20.25 | 0.95 | 0.99 | |||
| 3 | 9,010 | 35 | 1,490 | 758 | 947 | 900 | 0.492 | 0.570 | 50.32 | 14,900 | 3,380 | 26.61 | 38.40 | 20.75 | 0.94 | 0.94 | |||
| 4 | 9,160 | 33 | 1,490 | 762 | 944 | 900 | 0.495 | 0.573 | 51.86 | 15,820 | 3,270 | 27.03 | 39.40 | 20.95 | 0.93 | 0.95 | |||
| 5 | 8,860 | 66 | 1,430 | 764 | 944 | 898 | 0.450 | 0.538 | 56.90 | 21,100 | 2,700 | 26.17 | 46.00 | 21.58 | 0.94 | 1.00 | |||
| 6 | 11,850 | 89 | 1,455 | 752 | 948 | 897 | 0.490 | 0.570 | 64.96 | 20,300 | 3,200 | 34.93 | 49.50 | 27.18 | 1.03 | 1.04 | |||
| 7 | 10,520 | 50 | 1,440 | 749 | 948 | 896 | 0.475 | 0.557 | 62.22 | 21,050 | 2,960 | 31.04 | 48.60 | 24.73 | 0.98 | 1.02 | |||
| 8 | 9,650 | 55 | 1,430 | 746 | 948 | 894 | 0.474 | 0.556 | 60.56 | 21,200 | 2,860 | 29.36 | 47.40 | 23.40 | 0.96 | 1.01 | |||
| 11 | 6,760 | 119 | 1,400 | 742 | 878 | 853 | 0.410 | 0.505 | 49.03 | 20,620 | 2,395 | 19.92 | 42.20 | 17.50 | 0.89 | 0.96 | |||
| 12 | 7,990 | 92 | 1,450 | 753 | 878 | 857 | 0.430 | 0.520 | 52.50 | 19,920 | 2,645 | 23.56 | 43.90 | 20.08 | 0.93 | 0.98 | |||
| Avg | .... | 0.95 | 0.99 | ||||||||||||||||
| 4 | Gas | 1 | 7,840 | 44 | 1,454 | 711 | 937 | 842 | 0.492 | 0.740 | 38.33 | 12,254 | 3,120 | 18.78 | 36.95 | 18.90 | 0.95 | 0.92 | |
| 2 | 7,990 | 62 | 1,432 | 718 | 914 | 833 | 0.466 | 0.720 | 41.84 | 14,698 | 2,840 | 19.13 | 42.40 | 19.80 | 0.97 | 0.92 | |||
| 3 | 7,160 | 71 | 1,401 | 714 | 909 | 826 | 0.466 | 0.720 | 39.09 | 14,408 | 2,295 | 17.17 | 40.40 | 17.70 | 0.94 | 1.04 | |||
| 4 | 6,360 | 72 | 1,389 | 712 | 906 | 823 | 0.466 | 0.720 | 34.65 | 12,841 | 2,290 | 15.25 | 35.10 | 15.79 | 0.92 | 1.02 | |||
| 5 | 9,900 | 75 | 1,454 | 749 | 937 | 871 | 0.466 | 0.720 | 54.94 | 20,772 | 2,335 | 23.68 | 55.50 | 24.50 | 1.02 | 1.14 | |||
| 6 | 7,340 | 78 | 1,463 | 740 | 933 | 859 | 0.455 | 0.710 | 44.59 | 17,127 | 2,550 | 17.58 | 46.90 | 18.42 | 0.89 | 0.88 | |||
| 7 | 7,550 | 81 | 1,472 | 716 | 934 | 847 | 0.455 | 0.710 | 46.11 | 18,009 | 2,560 | 18.09 | 47.50 | 18.96 | 0.90 | 0.89 | |||
| Avg | .... | 0.94 | 0.97 | ||||||||||||||||
| 5 | Gas | 1 | 4,510 | 101 | 1,466 | 803 | 1,001 | 949 | 0.485 | 0.530 | 50.57 | 20,627 | 2,465 | 21.11 | 40.75 | 17.27 | 0.89 | 0.97 | |
| 2 | 4,800 | 103 | 1,473 | 825 | 1,025 | 969 | 0.485 | 0.530 | 54.41 | 22,310 | 2,450 | 22.40 | 44.00 | 18.30 | 0.91 | 0.98 | |||
| 3 | 5,610 | 88 | 1,477 | 836 | 1,049 | 988 | 0.495 | 0.535 | 57.96 | 22,040 | 2,625 | 26.27 | 46.00 | 21.25 | 0.97 | 1.04 | |||
| Avg | .... | 0.92 | 1.00 | ||||||||||||||||
| 6 | Gas | 1 | 14,910 | 5.1 | 1,781 | 666 | 1,004 | 986(j) | 0.470 | 0.595 | 88.56 | 22,740 | 3,840 | 45.66 | 90.60 | 47.80 | 1.04 | 1.00 | |
| 2 | 14,840 | 6.4 | 1,789 | 664 | 1,006 | 990 | 0.470 | 0.595 | 90.04 | 23,344 | 3,840 | 45.46 | 92.10 | 47.40 | 1.03 | 0.98 | |||
| Avg | .... | 1.02 | 0.99 | ||||||||||||||||
| 7 | Gas | 1 | 12,053 | 22 | 1,507 | 672 | 920 | 845 | 0.586 | 0.660 | 184.7 | 51,910 | 3,550 | 104.6 | 75.00 | 43.80 | 1.18 | 1.11 | |
| 2 | 9,300 | 41 | 1,433 | 753 | 948 | 903 | 0.570 | 0.650 | 138.6 | 43,875 | 3,160 | 74.1 | 52.40 | 30.85 | 1.11 | 1.14 | |||
| Avg | .... | 1.15 | 1.13 | ||||||||||||||||
| 8 | Gas | 1 | 16,970(i) | 128 | 598 | 818 | 880 | 0.323 | 0.762 | 21.45 | 16,958 | 2,090 | 4.82(f) | 127.90 | 29.30 | 0.86 | 0.96 | ||
| 2 | 23,800 | 64 | 510 | 788 | 872 | 0.365 | 0.788 | 19.85 | 11,491 | 2,750 | 6.77 | 114.20 | 39.80 | 1.01 | 0.95 | ||||
| 3 | 28,800 | 50 | 494 | 778 | 884 | 0.375 | 0.795 | 23.05 | 11,582 | 2,970 | 8.16 | 131.80 | 47.50 | 1.04 | 0.94 | ||||
| 4 | 36,700 | 34 | 480 | 789 | 929 | 0.370 | 0.790 | 30.28 | 16,994 | 3,290 | 10.43 | 174.00 | 61.10 | 1.04 | 0.91 | ||||
| 5 | 39,000 | 52 | 497 | 786 | 941 | 0.360 | 0.780 | 34.40 | 20,122 | 2,950 | 11.10 | 200.00 | 65.80 | 1.11 | 1.00 | ||||
| 6 | 42,500 | 53 | 512 | 786 | 958 | 0.360 | 0.780 | 38.44 | 18,442 | 2,870 | 12.09 | 224.00 | 71.60 | 1.10 | 1.07 | ||||
| 7 | 50,900 | 33 | 473 | 775 | 980 | 0.368 | 0.788 | 44.72 | 18,163 | 3,220 | 14.45 | 258.00 | 85.00 | 1.09 | 1.00 | ||||
| Avg | .... | 1.04 | 0.98 | ||||||||||||||||
| 9 | Gas | 1 | 12,470 | 26 | 1,725 | 749 | 978 | 990(j) | 0.480 | 0.545 | 81.56 | 21,200 | 3,823 | 44.60 | 79.50 | 44.50 | 1.05 | 1.03 | |
| 2 | 12,450 | 32 | 1,652 | 745 | 973 | 995 | 0.471 | 0.540 | 83.01 | 23,000 | 3,600 | 44.63 | 81.60 | 44.90 | 1.08 | 1.07 | |||
| 3 | 11,900 | 16 | 1,786 | 741 | 977 | 1,000 | 0.480 | 0.545 | 79.07 | 20,150 | 3,910 | 42.71 | 77.00 | 42.50 | 1.01 | 1.00 | |||
| 4 | 11,530 | 46 | 1,711 | 759 | 975 | 1,007 | 0.445 | 0.516 | 85.90 | 25,850 | 3,320 | 41.48 | 88.30 | 43.50 | 1.03 | 1.04 | |||
| Avg | .... | 1.04 | 1.03 | ||||||||||||||||
| 10 | Oil | 1 | 21,200 | 26 | 1,705 | 670 | 914 | 898 | 0.430 | 0.750 | 30.99 | 9,252 | 3,340 | 14.55 | 87.00 | 41.65 | 0.95 | 0.99 | |
| 2 | 20,400 | 21 | 1,695 | 677 | 912 | 898 | 0.437 | 0.753 | 28.47 | 8,187 | 3,475 | 13.98 | 79.90 | 39.83 | 0.95 | 0.98 | |||
| 3 | 21,600 | 38 | 1,740 | 691 | 910 | 900 | 0.420 | 0.742 | 34.57 | 11,168 | 3,100 | 14.82 | 98.00 | 42.90 | 0.93 | 1.00 | |||
| Avg | .... | 0.94 | 0.99 | ||||||||||||||||
| 11 | (k) | 1 | 3,140 | 111 | 1,037 | 573 | 670 | 682 | 0.390 | 0.665 | 15.82 | 11,701 | 1,388 | 8.67 | 46.90 | 11.10 | 0.67 | 1.08 | |
| 2 | 4,320 | 74 | 1,038 | 570 | 677 | 686 | 0.425 | 0.691 | 13.92 | 8,312 | 1,702 | 5.07 | 39.65 | 14.72 | 0.87 | 1.16 | |||
| 3 | 3,840 | 91 | 1,103 | 593 | 691 | 703 | 0.395 | 0.667 | 19.06 | 12,276 | 1,585 | 5.35 | 56.25 | 13.51 | 0.77 | 0.98 | |||
| Avg | .... | 0.77 | 1.07 | ||||||||||||||||
| 12 | Oil | 1 | 10,780 | 45 | 1,457 | 474 | 750 | 716 | 0.490 | 0.706 | 48.48 | 16,209 | 2,990 | 24.88 | 56.10 | 29.50 | 0.95 | 1.04 | |
| 2 | 8,770 | 63 | 1,399 | 470 | 729 | 689 | 0.475 | 0.695 | 41.66 | 15,531 | 2,690 | 20.03 | 49.20 | 24.10 | 0.91 | 1.02 | |||
| Avg | .... | 0.93 | 1.03 | ||||||||||||||||
| 13 | Gas | 1 | 9,300 | 17 | 1,560 | 712 | 915 | 897 | 0.590 | 0.631 | 56.36 | 13,786 | 4,060 | 34.53 | 41.45 | 25.90 | 1.02 | 0.99 | |
| 14 | Gas | 1 | 7,060 | 28 | 1,700 | 738 | 903 | 897 | 0.560 | 0.595 | 46.10 | 11,626 | 3,940 | 26.09 | 36.00 | 20.80 | 0.94 | 0.91 | |
| 15 | Gas | 1 | 9,150 | 15 | 1,750 | 734 | 901 | 894 | 0.580 | 0.630 | 52.46 | 12,080 | 4,310 | 31.01 | 42.35 | 25.50 | 0.99 | 0.93 | |
| 16 | Gas | 1 | 9,300 | 26 | 1,623 | 704 | 898 | 883 | 0.565 | 0.595 | 58.46 | 14,630 | 3,980 | 34.45 | 45.60 | 27.45 | 0.99 | 0.98 | |
| Avg | .... | 0.98 | 0.96 | ||||||||||||||||
| 17 | Gas | 1 | 9,810 | 59 | 1,505 | 712 | 892 | 872 | 0.415 | 0.630 | 42.19 | 15,000 | 2,815 | 16.89 | 74.00 | 30.20 | 0.92 | 0.94 | |
| 18 | Gas | 1 | 9,330 | 57 | 1,480 | 737 | 950 | 925 | 0.417 | 0.580 | 39.99 | 14,062 | 2,850 | 17.41 | 70.10 | 31.20 | 0.97 | 1.00 | |
| 2 | 9,350 | 59 | 1,482 | 735 | 960 | 930 | 0.417 | 0.580 | 40.60 | 14,402 | 2,820 | 17.46 | 70.50 | 31.20 | 0.96 | 1.01 | |||
| 3 | 8,310 | 86 | 1,415 | 685 | 905 | 870 | 0.395 | 0.560 | 39.79 | 16,222 | 2,460 | 15.52 | 72.10 | 28.75 | 0.95 | 1.05 | |||
| Avg | .... | 0.96 | 1.02 | ||||||||||||||||
| 19 | Oil | 1 | 9,120 | 95 | 1,382 | 825 | 850 | 879 | 0.45 | 0.596 | 87.50 | 37,350 | 2,360 | 32.97 | 79.00 | 30.38 | 0.90 | 1.08 | |
| Grand | Avg | .... | 0.969 | 0.992 | |||||||||||||||
| (a) | At bridge wall. | Average Deviation | ................ | 6.85 % | 5.30 % |
| (b) | With high velocity thermocouples. | Maximum Deviation | ................ | 33 % | 16 % |
| (c) | Estimated from average oil temperature, inside coefficient with allowance for coke deposit. | % of Tests Between | 0 and 2 % Deviation.... | 17.7 % | 31.8 % |
| (d) | Net heat input from combustion of the fuel, air preheat, and recirculation if any. | 0 and 4 % Deviation.... | 36.5 % | 53.0 % | |
| (e) | Based on flue gas duty, except for Furnaces Nos. 1 and 8. | ||||
| (f) | Estimated from oil side. Applies only to furnaces Nos. 1 and 8. | ||||
| (g) | Wilson, Lobo, and Hottel Empirical Radiant Equation. | ||||
| (h) | Temperatures for Furnace No. 2 are average oil temperatures. | ||||
| (i) | Based on exposed tube surface. | ||||
| (j) | Actual tube skin thermocouple measurements. | ||||
| (k) | Fuel = Products of combustion from Furnace No. 10. |
The actual heat to the oil is obtained by subtracting the enthalpy of the flue gas leaving the radiant section from the enthalpy of the entering fuel and air, and then subtracting the estimated external losses, plus the direct radiant heat from the combustion chamber absorbed by the first rows of the convection section. The latter item is obtained by a convection section heat balance , gas side versus oil side, in which the heat lost by the gas is considered between the actually measured true gas temperature of the gases entering and leaving the section. A summary of the test data required and a short outline of the method of calculation are included in the Appendix.
 |
Table III gives a summary of the test data and calculations for all eighty-five tests which have been used as an independent check on the validity of the derived theoretical equation. The ratio of the actual heat absorbed by the oil in the radiant section to that predicted by both the empirical and theoretical equations is given for each of the individual tests. The deviations of any test from the average deviations for a given furnace can thus be readily seen.
In order to arrive at a definite conclusion regarding the respective merits of the Wilson, Lobo and Hottel empirical equation and the theoretical equation, the heat absorbed by the oil in the radiant section as predicted by these two equations has been compared to the actually observed heat absorption.
 |
 |
The radiant section will be defined as that section in which the heat is liberated and in which the heat transfer is primarily by radiation from the hot gas mass and the hot refractory surfaces. The cold or ultimate heat-receiving surface is considered to consist of those tubes which can "see" to a greater or less extent the main gas mass. This emphasis has been made because in the case of certain furnaces the first rows of tubes in the convection section can see the main gas mass. The plane area * of these tubes, Acp, must be considered as a part of the radiant section equivalent cold plane surface, a Acp. In furnaces where the convection section is placed behind a bridge wall, out of sight of the main gas mass, the projected area of the convection section is not considered to be part of the radiant section cold surface.
*In a bank of three or more rows of tubes a = 1.0, and Acp = aAcp.
It may be seen from Table III that in practically every case the equation presented in this paper correlates the test data better than the empirical equation even though the furnace tests used to determine the constants of the empirical equation are included in the present data. The maximum deviation has been reduced from 335 to 16%. These facts are perhaps best illustrated by Figures Nos. 9 and 10, which show the spread of the data using both methods of correlation. Inasmuch as the data represent plant tests, it is suspected that the larger deviations may be due to inaccuracies in the data and not to any fundamental fault in the radiant equation. It is significant that using the theoretical equation the greatest deviations are not confined to any one furnace but seem to be well distributed. Again, furnace No. 4, the worst case, shows deviations of -11% and -12% and +14%, indicating that the data on this one furnace are probably less reliable than the average. Actually, the temperature of the gases leaving the radiant section of this furnace was determined at only two points instead of by a complete traverse. Since in many cases it is difficult to judge exactly the accuracy of the plant data, no attempt has been made to segregate and give more weight to the better data. The number of tests available for this study is hardly large enough for a rigid statistical analysis, but for some generalizations are justified. For instance, considering the data in their entirety, Figures Nos. 10 and 12(A) indicate that the deviations between the observed and the calculated heat absorption occur in a random manner and are not peculiar to any one fiurnace, even though the ratio of effective refractory to effective cold surface, (Ar/aAcp), varied fourteen-fold for the furnaces investigated.
Figure 11 (B) (C) (D) and Figure 12 (B) (C) (D) are given in order to permit visualizing the effect of some of the variables on the results obtained by the two correlations.
The effect of excess air is shown in Figures 11 (B) and 12 (B). It should be remembered that although the percentage of excess air varied less than 10% to more than 170%, other factors may likewise have been varying at the same time. In general, the empirical equation appears to predict correctly the heat absorption by the oil in the radiant section in the excess air range from 10% to 80%, the more usual commercial range. Above 80% it predicts heat absorptions which are 10% to 13% too high. Over this range, 10% to 170%, the theoretical equation shows no significant trend. As previously pointed out, the use of an air-fuel ratio is open to criticism and the trend may be due to this factor.
Figures 11 (C) and 12 (C) classify the data according to average radiant rate based on circumferential tube surface, B.t.u. per hour per sq. ft. In those furnaces with a double row of radiant tubes, the rate has been taken as the average first row rate. Here, again, the theoretical equation shows no significant trend over the range 3,000 to 51,000 B.t.u. per hour per sq. ft. The empirical equation shows signs of breaking down at rates below 4,000 and predicts radiant section heat absorption 10% in excess of the true figure at that point. Only two tests are available at rates between 3,000 and 4,000 but they confirm the trend and indicate that the heat absorbed by the oil, as calculated by the empirical equation, may be almost 40% high in this range.
Figures 11 (D) and 12 (D) give another indication of the range of the furnace data, but have significance only in that they give an indication of the theoretical flame temperature. These figures show that over the wide range of t'f, the pseudo-theoretical flame temperature, the deviations have no definite trend. It is obvious, therefore, that petroleum heaters can be designed by means of the new equation for fuels of widely different heating values as a low pseudo-flame temperature may mean either a fuel of low grade, or a high heating value fuel degraded with excess air or recirculated inert gas. Since most of these tests have been made with very similar fuels, the trend shown in Figure 11 (D) is probably due to the composite effect of rate and excess air discussed above.
 |
 |
The theoretical radiant equation as developed in this paper is recommended for the solution of heat transfer problems in the radiant section of tubular heaters using fuel oil or gaseous fuel.
The equation is believed to be valid for any condition of air preheat, inert gas recirculation, percentage of excess air, or radiant rate. The effect of furnace volume on the amount of heat liberation necessary to maintain any given radiant rate is adequately handled by the use of the flame emissivity as outlined previously. The results indicate that the f plot represents an accurate and simple method of simultaneously allowing for the effect of flame emissivity and the amount of refractory surface present in the radiant section.
The Wilson, Lobo, and Hottel empirical equation is not recommended for use on furnaces differing widely from those used to determine the constants of the equation. However, the equation may be used with safety on box-type heaters (see Figures 16, 17, 18, 20 and 21) when the greatest accuracy is not required and subject to the following qualifications :
| 1. | Fuel oil or cracked refinery gas as fuel; |
| 2. | Radiant rates between 5,000 and 30,000 B.t.u./hr./sq.ft. of circumferential tube area ; |
| 3. | Per cent excess air between 5% and 80%; |
| 4. | Tube skin temperatures not closer than 400� F, to the temperature of the flue gas leaving the radiant section ; |
| 5. | Length of the radiant beam, L, greater than 15 feet. |
| Ao | = | total outside tube area exposed to radiation, sq.ft. |
| AR | = | effective refractory area, sq.ft. |
| A'R | = | actual refractory area, sq.ft. |
| AT | = | total wall area in combustion section, sq.ft. |
| Acp | = | area of plane replacing tubes, sq.ft. |
| C | = | actual firing rate of fuel/sq.ft. of exposed tube area, lbs./hr./sq.ft. |
| Co | = | equivalent firing rate of good bituminous coal/sq.ft. of projected tube area, lbs./hr./sq.ft. |
| CA | = | firing rate based on projected tube area, lbs./hr./sq.ft. |
| E | = | effectiveness factor of the cold surface |
| Frc | = | fraction of all the radiation emitted from all the refractory in all directions, which, if not absorbed by the gas, would hit cold surface, aAcp |
| FS | = | angle-emissivity factor |
| G | = | air-fuel ratio, lbs. air /lb. of fuel |
| H | = | total net heat input to combustion chamber, B.t.u./hr. |
| hc | = | convection coefficient, B.t.u./hr./sq.ft./�F. |
| L | = | mean length of radiant beam, feet |
| N | = | hourly heat capacity, B.t.u./hr./�F. |
| Pe | = | emissivity of tube surface |
| Pf | = | emissivity of flame |
| PCO2 | = | partial pressure of CO2, atmospheres |
| PH2O | = | partial pressure of water vapor, atmospheres |
| MCPavg. | = | mean molal heat capacity between 60� and temperature, tg |
| Q | = | net heat liberated from combustion of the fuel, B.t.u./hour |
| q | = | heat transferred to oil, B.t.u./hour |
| q' | = | heat transferred by radiation, B.t.u./hour |
| q" | = | net heat transferred to all surfaces in the radiant section, B.t.u./hour |
| Se | = | equivalent "effective" heating surface, sq.ft. |
| Tg | = | temperature of products of combustion leaving combustion chamber, �F. + 460� |
| Ts | = | tube skin temperature, �F. + 460� |
| t | = | temperature, �F. |
| tg | = | temperature of flue gas leaving combustion chamber, �F. |
| t'f | = | Pseudo-flame temperature, �F. |
| a | = | factor by which Acp must be reduced to obtain effective cold surface, aAcp (effective tube area) |
| b | = | fraction of total net heat input lost from the external furnace walls |
| f | = | overall exchange factor |
| m | = | fraction of heat available above 60� F. absorbed by cold surfaces in the combustion chamber |
|
|
|
| 1. | Hottel, Trans. A.I.Ch.E. 19, 173 (1927); Ind. Eng. Chem. 19, 888 (1927) |
| 2. | Wilson, Lobo, Hottel, Ind. Eng. Chem. 24, 486 (1932) |
| 3. | Hudson, Engineer 70, 523 (1890) |
| 4. | Orrok, Trans. A.S.M.E. 1148 (1925) |
| 5. | Hottel, Unpublished notes on Radiant Heat Transmission, Mass. Inst. of Tech. (1938) |
| 6. | DeBaufre, Trans. A.S.M.E. 53 (14), 253 (1931) |
| 7. | Mekler, Nat. Pet. News 30 (30), R355 (1938) |
| 8. | Hottel, Trans. A.S.M.E., Fuels Steam Power 53 (14), 265 (1931) |
| 9. | Hottel, Unpublished notes on Radiant Heat Transmission, Mass. Inst. of Tech. (1938) |
| 10. | Hottel, in Chem. Eng. Handbook 1, 888 (1934) |
| 11. | Hottel, Ibid. 1, 910 (1934) |
| 12. | Hottel, Ibid. 1, 892 (1934) |
The authors gratefully acknowledge the helpful suggestions offered during the course of the investigation by Mr. J. H. Rickerman.
| Component | Mol PerCent | |
| CH4 | ................................... | 37.0 |
| C2H4 | ................................... | 4.0 |
| C2H6 | ................................... | 22.0 |
| C3H6 | ................................... | 8.0 |
| C3H8 | ................................... | 23.0 |
| C4H10 | ................................... | 6.0 |
| ____ | ||
| 100.0 |
Lower heating value per lb. at 60� F. 20,557 B.t.u. (Higher heating value 22,400 B.t.u.)
Specific gravity relative to air, 1.06
Specific volume at 60� F. and 14.7 lb./sq.in. 0.0807 lb./ft.3
Combustion calculations are based on air at 60� F. and 50% relative humidity.
| Component | Wt. PerCent | |
| C | ................................... | 85.0 |
| H2 | ................................... | 12.0 |
| S | ................................... | 1.5 |
| O2 | ................................... | 0.7 |
| N2 | ................................... | 0.8 |
| ____ | ||
| 100.0 |
Lower heating value per lb. at 60� F. 17,130 B.t.u.
Steam for atomization, 0.3 lb./lb. fuel oil
Air at 60� F. and 50% relative humidity.
| A. | Quantities: | |
| 1. | Fuel. | |
| 2. | Oil through furnace. | |
| 3. | Steam used for atomization, if any. | |
| B. | Temperatures: | |
| 1. | Oil to and from various sections of furnace. | |
| 2. | Flue gas from radiant section, determined by high velocity couple traverse, reading being taken about every two feet across furnace. | |
| 3. | Flue gas from convection section or after bank of convection tubes through which combustion gases first pass, determined by high velocity couple traverse. | |
| 4. | Air, both atmospheric and preheated, if any. | |
| 5. | Fuel. | |
| 6. | Surface of furnace for estimation of radiant losses. | |
| 7. | Steam used for atomization, if any. | |
| C. | Analysis: | |
| 1. | Fuel, heating value and proximate analysis. | |
| 2. | Flue gas from radiant section by Orsat analysis of samples drawn through water-cooled sampling tube at intervals comparable to those used in temperature measurements. | |
| 3. | Flue gas from same convection section section bank after which temperature (3) was measured, sample taken and analized as above. | |
| D. | Humidity of Atmospheric Air. | |
Due to the fact that in petroleum heaters it is often difficult to determine accurately the heat absorbed by the oil in the radiant section from the oil side because of unknown heat of reaction, vaporization, etc., it is essential in most cases to obtain this figure by heat balance from the flue gas side, determining also by heat balance, as mentioned in the paper, any direct radiation from the combustion box to the convection section. Thus, the balance may be shown as follows:
| Heat Input: | ||
| 1. | Heat of combustion of fuel. | |
| 2. | Heat in air used for combustion. | |
| 3. | Heat in steam used for atomization, if any. | |
| 4. | Heat in recirculated flue gases, if any. | |
 |
 |
| Heat Output: | ||
| 1. | Heat in flue gases leaving radiant section. | |
| 2. | Heat to oil in radiant section (determined by difference). | |
| 3. | Heat to external losses. | |
| 4. | Heat radiated from combustion box to convection section (determined by heat balance on part or all of convection section). | |
 |
 |
 |
 |
 |
 |
 |
 |